【Python】Numpyのみでニューラルネットワークを実装する

環境
仕様
計算フローと計算式
サンプルコード
コードの解説
まとめ

環境

Python 3.9
Numpy 1.21.5

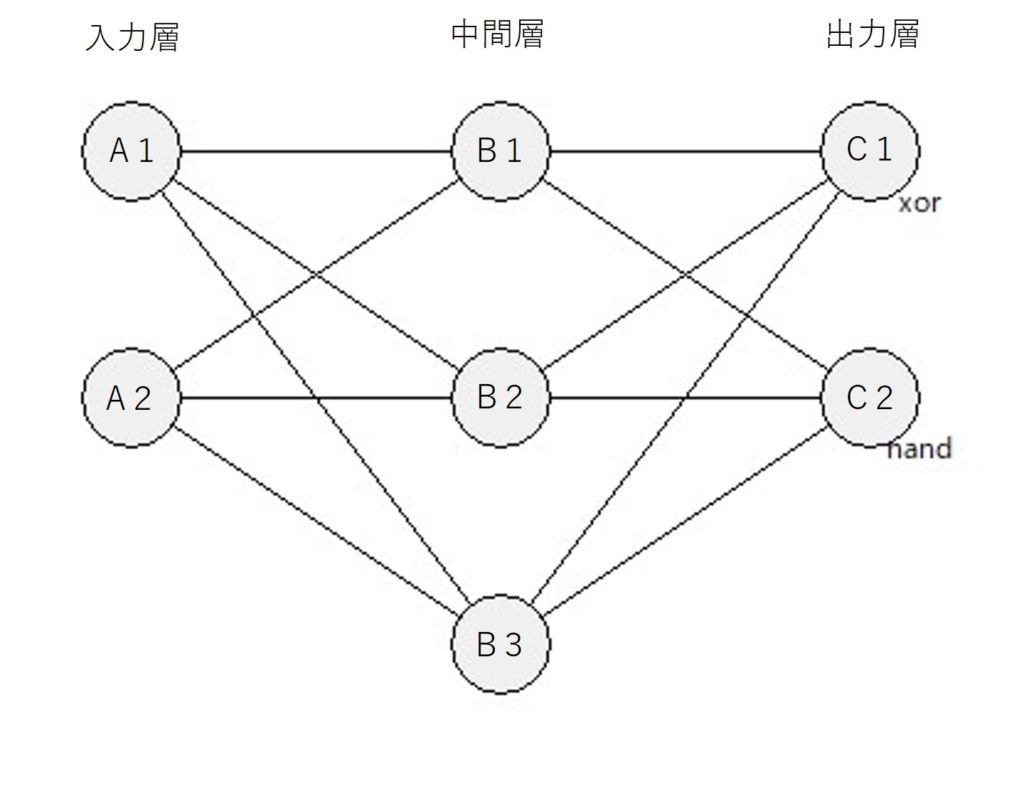
仕様

入力層２・中間層３・出力層２
xor, nandを学習する
中間層・出力層の活性化関数はシグモイド関数を使用する
バイアスなし

A1	A2	C1：xor	C2：nand
0	0	0	1
0	1	1	1
1	0	1	1
1	1	0	0

図2：真理値表（期待値）

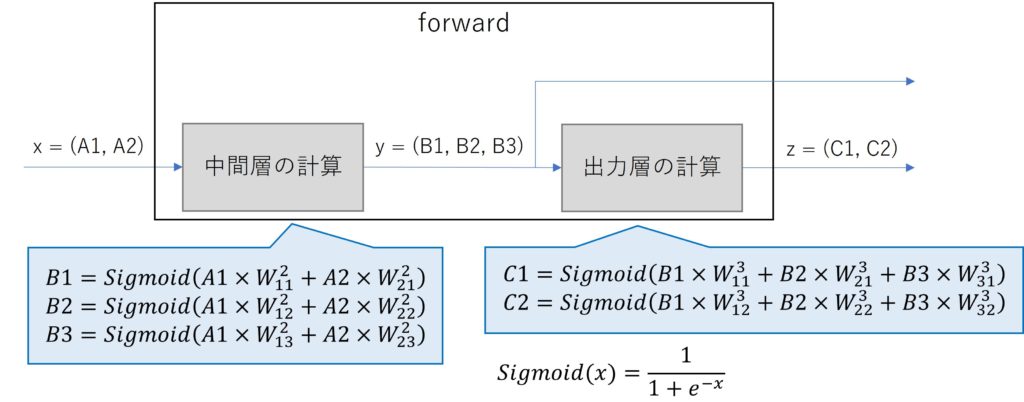
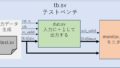
計算フローと計算式

forward

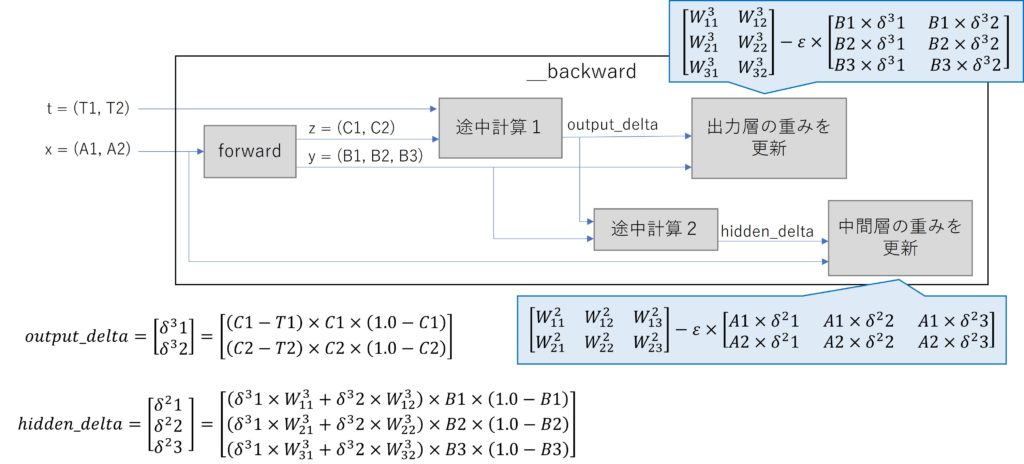
backward

サンプルコード

forwardとtrainのメソッドを持つクラスNnを作成します

trainで学習を行い、forwardで学習結果を確認します

引数は以下です

train(<入力データ>, <教師データ>, <学習係数>, <学習回数>)
forward(<入力データ>)

simple_nn.py

import numpy

class Nn:
    def __init__(self, n_input, n_hidden, n_output):
        self.hidden_weight = numpy.random.random_sample((n_hidden, n_input))
        self.output_weight = numpy.random.random_sample((n_output, n_hidden))

    def __sigmoid(self, x):
        return 1.0 / (1.0 + numpy.exp(-x))

    def forward(self, x):
        y = self.__sigmoid(numpy.sum(x*self.hidden_weight, axis=1))
        z = self.__sigmoid(numpy.sum(y*self.output_weight, axis=1))
        return y, z

    def __backward(self, x, t, epsilon):
        y, z = self.forward(x)

        # update output_weight
        output_delta = (z - t) * z * (1.0 - z)
        _output_weight = self.output_weight
        self.output_weight -= epsilon * y * output_delta.reshape((-1, 1))

        # update hidden_weight
        hidden_delta = numpy.sum(output_delta * _output_weight.T, axis=1) * y * (1.0 - y)
        self.hidden_weight -= epsilon * x * hidden_delta.reshape((-1, 1))

    def train(self, X, T, epsilon, epoch):
        for _ in range(epoch):
            for i in range(X.shape[0]):
                self.__backward(X[i, :], T[i, :], epsilon)

if __name__ == '__main__':
    X = numpy.array([[0, 0], [0, 1], [1, 0], [1, 1]])
    T = numpy.array([[0, 1], [1, 1], [1, 1], [0, 0]])

    input_size = 2
    hidden_size = 3
    output_size = 2
    epsilon = 0.5
    epoch = 100000

    nn = Nn(input_size, hidden_size, output_size)
    nn.train(X, T, epsilon, epoch)

    for i in range(X.shape[0]):
        _, z = nn.forward(X[i, :])
        print("In  {}".format(X[i, :]))
        print("Act {}".format(z))
        print("Exp {}\n".format(T[i, :]))

実行結果

シードが固定されていないので、学習結果が多少変わると思います。

In：入力データ、Act：得られた出力、Exp：期待値

In  [0 0]
Act [0.0211309  0.99999496]
Exp [0 1]

In  [0 1]
Act [0.97426658 0.98324979]
Exp [1 1]

In  [1 0]
Act [0.97425345 0.9832464 ]
Exp [1 1]

In  [1 1]
Act [0.03027528 0.02259229]
Exp [0 0]

コードの解説

    def __init__(self, n_input, n_hidden, n_output):
        self.hidden_weight = numpy.random.random_sample((n_hidden, n_input))
        self.output_weight = numpy.random.random_sample((n_output, n_hidden))

初期化メソッドです。hidden_weightは中間層の重み、output_weightは出力層の重みです。

numpy.random.random_sampleで一様分布の乱数を生成して初期値を決定します

    def __sigmoid(self, x):
        return 1.0 / (1.0 + numpy.exp(-x))

シグモイド関数のメソッドです。計算結果を返します。

    def forward(self, x):
        y = self.__sigmoid(numpy.sum(x*self.hidden_weight, axis=1))
        z = self.__sigmoid(numpy.sum(y*self.output_weight, axis=1))
        return y, z

forwardメソッドです。入力に重みをかけて足し合わせ、シグモイド関数に入れます。

中間層と出力層の出力を返します。

    def train(self, X, T, epsilon, epoch):
        for _ in range(epoch):
            for i in range(X.shape[0]):
                self.__backward(X[i, :], T[i, :], epsilon)

学習メソッドです。epochで与えた数だけself.__backwardを実行します。

    def __backward(self, x, t, epsilon):
        y, z = self.forward(x)

        # update output_weight
        output_delta = (z - t) * z * (1.0 - z)
        _output_weight = self.output_weight
        self.output_weight -= epsilon * y * output_delta.reshape((-1, 1))

        # update hidden_weight
        hidden_delta = numpy.sum(output_delta * _output_weight.T, axis=1) * y * (1.0 - y)
        self.hidden_weight -= epsilon * x * hidden_delta.reshape((-1, 1))

backwardのメソッドです。

forwardメソッドで中間層、出力層の出力y, zを取得します。

教師データt, 出力層の出力zから中間データoutput_deltaを計算します。
中間データoutput_delta、中間層の出力y、学習係数epsilonでoutput_weightを更新します。

中間データoutput_delta, 出力層の重み_output_weight, 中間層の出力yから中間データhidden_deltaを計算します。
中間データhidden_delta, 入力データx、学習係数epsilonでhidden_weightを更新します。

if __name__ == '__main__':
    X = numpy.array([[0, 0], [0, 1], [1, 0], [1, 1]])
    T = numpy.array([[0, 1], [1, 1], [1, 1], [0, 0]])

    input_size = 2
    hidden_size = 3
    output_size = 2
    epsilon = 0.5
    epoch = 100000

    nn = Nn(input_size, hidden_size, output_size)
    nn.train(X, T, epsilon, epoch)

    for i in range(X.shape[0]):
        _, z = nn.forward(X[i, :])
        print("In  {}".format(X[i, :]))
        print("Act {}".format(z))
        print("Exp {}\n".format(T[i, :]))

Xが入力データ、Tが教師データです。

nn = Nn(<入力層の数>, <中間層の数>, <出力層の数>)で初期化して、nn.train()で学習を行います。

学習後、nn.forward()で結果を確認します。